Jumat, 05 Februari 2016

Barisan dan deret


Di dalam Matematika, sebuah barisan bilangan adalah daftar terurut dari suatu bilangan. Seperti layaknya himpunan, suatu barisan juga memiliki anggota (elemen) yang biasanya disebut suku. Contoh suatu barisan adalah sebagai berikut:
  1. (1, 1, 1, 1, 1, \cdots )
  2. (1, 2, 3, 4, 5, 6 , \cdots)
  3. (1, 4, 9, 16, \dotsc)
  4. (1, 2, 4, 8, 16, \dotsc)
Barisan bilangan bilangan bisa berupa barisan Aritmetika maupun barisan Geometri. Suku-suku yang berdekatan dari suatu barisan Aritemetika selalu memiliki selisih yang tetap/konstan, biasa disebut dengan beda. Dalam barisan geometri hasil bagi suku-suku yang saling berdekatan selalu tetap/konstan, yang disebut dengan rasio.
Deret bilangan merupakan penjumlahan suku-suku dari barisan yang bersesuaian. Contoh deret bilangan yang dibentuk dari barisan-barisan diatas adalah sebagai berikut:
  1. 1 + 1 + 1 + 1 + 1 + \dotsb
  2. 1 + 2 + 3 + 4 + 5 + \dotsb
  3. 1 + 4 + 9 + 16 + 25 + \dotsb
  4. 1 + 2 + 4 + 8 + 16 + \dotsb
Deret aritemtika dapat dibentuk dari barisan aritmetika, dan deret geometri dapat diperoleh dari barisan geometri

        Barisan Aritmetika

        Barisan aritmetika adalah barisan yang selisih antara suku-suku yang berdekatan tetap/konstan.
        Rumus umum suku ke-n adalah U_n = a + (n-1)b
        dengan a=U_1 adalah suku awal atau suku pertama dan b=U_2 - U_1 = U_3 - U_2 = \dotsb merupakan selisih suku-suku yang berdekatan.
        Jumlah angka pada seluruh barisan:  S_n = \frac {n} {2} \times (a + U_n)

        Barisan Geometri

        U_{n} = ar^{n-1}
        r = \frac {U_{2}} {U_{1}} = \frac {U_{3}} {U_{2}}
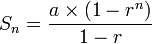
        S_n = \frac {a\times (1-r^n)} {1-r}

        Semoga bermanfaat ^^
        Fromhttps://id.m.wikibooks.org/wiki/Subjek:Matematika/Materi:Barisan_dan_deret
        Diposting oleh di

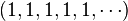
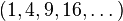
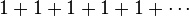
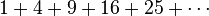
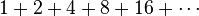
        Tidak ada komentar:

        Posting Komentar

        Langganan: Posting Komentar (Atom)